⦁ 이분법의 개념


⦁ 이분법 구현
def bisection(f, a, b, nmax, eps):
fa, fb = f(a), f(b)
if np.sign(fa) == np.sign(fb):
print("input: ", a, b, fa, fb)
print("function has same signs at a and b")
error = b - a
for n in range(nmax):
error = error/2
c = a + error
fc = f(c)
print ("{:<4} {:<40} {:<40} {:<40}".format(n, c, fc, error))
if np.abs(error) < eps:
return
if np.sign(fa) != np.sign(fc):
b = c
fb = fc
else:
a = c
fa = fc
# 함수 정의
f = lambda x: x**2 - 2
# 이분법 실행
bisection(f, 0, 2, 100, 10e-10)
⦁ 뉴턴법의 개념


⦁ 뉴턴법 구현
def newton(f, fpx, x, nmax, e, d):
fx = f(x)
print(0, x, fx)
for n in range(1, nmax):
fpx = fp(x)
if np.abs(fpx) < d: # 언더플로 방지
print("small derivative")
return
d = fx/fpx
x = x - d
fx = f(x)
print(n, x, fx)
if np.abs(d) < e:
print("convergence")
return
f = lambda x: 3*x + np.cos(x) - 5
fp = lambda x: 3 - np.sin(x)
newton(f, fp, 2, 30, 1e-6, 1e-8)
⦁ 할선법의 개념
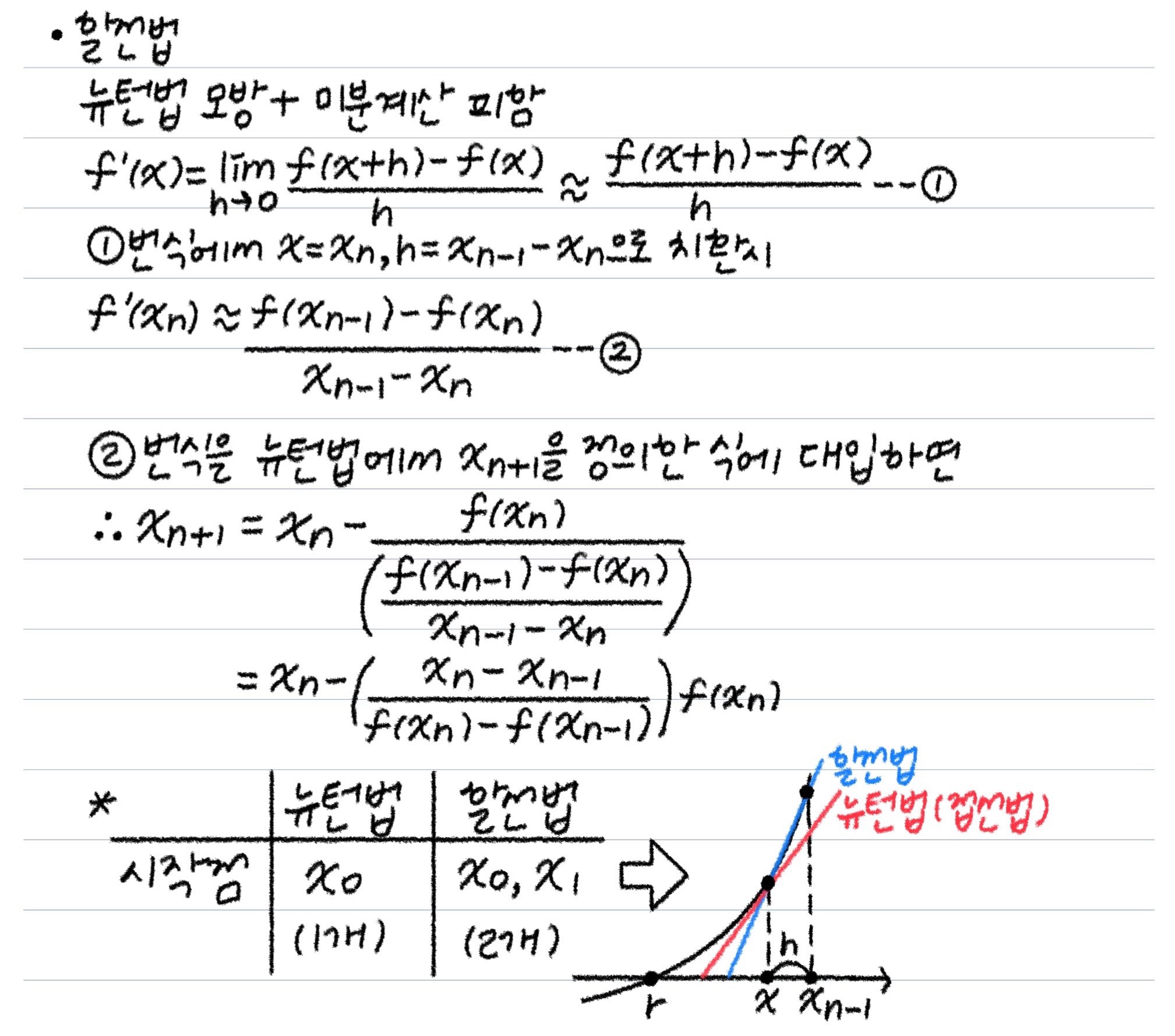
⦁ 할선법 구현
def secant(f, a, b, nmax, e):
fa = f(a)
fb = f(b)
if np.abs(fa) > np.abs(fb):
a, fa, b, fb = b, fb, a, fa
print(0, a, fa)
print(1, b, fb)
for n in range(2, nmax):
if np.abs(fa) > np.abs(fb):
a, fa, b, fb = b, fb, a, fa
d = (b - a)/(fb - fa)
b = a # b 업데이트
fb = fa
d = d*fa
if np.abs(d) < e:
print("convergence")
return
a = a - d # a 업데이트
fa = f(a)
print(n, a, fa)
f = lambda x: 3*x + np.cos(x) - 5
secant(f, 0, 2, 30, 1e-6)'수치해석' 카테고리의 다른 글
| 리처드슨 보외법, 롬베르크 알고리즘 (0) | 2024.01.08 |
|---|---|
| 보간법 (0) | 2024.01.03 |
| 순수 가우스 소거법 알고리즘 (0) | 2024.01.02 |
| 부동소수점 표현 (0) | 2024.01.02 |
| 테일러 급수 (0) | 2024.01.02 |



